1.
Pangkat Bulat
Positif
n adalah sebuah bilangan bulat positif dan a adalah
bilangan real, maka an didefinisikan sebagai perkalian n faktor yang
masing-masing faktornya a.
Sifat-sifat bilangan berpangkat bulat positif.
a.
am x an = am+n
b.
am/an
= am-n, a tidak sama dengan nol
c.
(am)n
= amxn
d.
(ab)n
= an. bn
e.
(a/b)n
= an/bn , b tidak sama dengan nol
2.
Pangkat bulat negatif dan pangkat nol
Sifat-sifat bilangan berpangkat bulat negatif :
a.
a0 = 1 , a tidak sama
dengan nol
b.
a-n = 1/ an
c.
(b/a)-n
= (a/b)n
3.
Pangkat pecahan
n bilangan positif ( n > 1 )
a dan b bilangan riil
B. Akar
1.
Bentuk akar adalah akar dari suatu
bilangan yang nilainya merupakan bilangan irasional.
2.
Secara umum dituliskan sebagai
berikut.
Dimana :
n = pangkat
m = indeks
3. Operasi aljabar
bentuk akar
4. Merasionalkan penyebut pecahan bentuk
akar
C. Logaritma
1.
Logaritma sebagai invers dari
perpangkatan
Logaritma sebagai bilangan x dengan bilangan pokok a (ditulis alog
x) adalah eksponen bilangan berpangkat yang menghasilkan x jika adipangkatkan
dengan eksponen itu. Dirumuskan dengan :
alog x = n artinya x = an
untuk a > 0, a tidak sama dengan 1 dan x > 0
2.
Sifat-sifat logaritma
Untuk a > 0, a tidak sama dengan 1, b ? 0, dan c = 0, pada logaritma
berlaku sifat-sifat berikut :
alog x + alog y = alog x.y
alog x - alog y = alog x/y
alog xn = n alog x
a pangkat alog x = x
a pangkat n log xm = m/n . alog
x
Sumber lain:





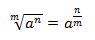

















0 komentar:
Posting Komentar