Dalam
matematika sering digunakan lambang-lambang yang umum dikenal oleh
matematikawan. Sering kali pengertian lambang ini tidak dijelaskan, karena
dianggap maknanya telah diketahui. Hal ini kadang menyulitkan bagi mereka yang
awam.
Lambang
matematika dipilah menjadi 3 jenis:
-
Lambang-lambang untuk bilangan-bilangan, kuantitas-kuantitas, peubah-peubah
(variabel) atau obyek-obyek. Masuk kategori ini adalah lambang pada
fungsi-fungsi trigonometri, pangkat, akar, logaritma atau lambang untuk
mendanai peubah.
-
Lambang-lambang operasi yang menggambarkan operasi terhadap bilangan. Masuk
kategori ini adalah: penambahan, pengurangan, pembagian, perkalian, dan
lambang-lambang dalam himpunan, faktorial, integral dan diferensial.
-
Lambang-lambang hubungan yang menggambarkan sesuatu ditetapkan. Lambang sama
dengan +) dan ketidaksamaan (< dan >), nisbah (ratio).

: Operasi penjumlahan

: Operasi perkalian
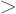
: Lebih besar dari. Misalnya 5 lebih besar dari 2, tulis


: Lebih kecil dari. Misalnya 3 lebih kecil dari 4, tulis

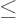
: Lebih kecil atau sama dengan
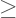
: Lebih besar atau sama dengan
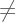
: Tidak sama dengan. Misalnya


: Himpunan bilangan bulat. Berasal dari kata “Zahlen”

: Himpunan bilangan asli. Natural number
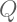
: Himpunan dari semua bilangan rasional. Quotients of integers

: Himpunan semua bilangan real

: Himpunan semua bilangan kompleks
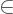
: Anggota dari.

, artinya 5 adalah anggota dari


: Bukan anggota dari.
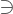
: Sedemikian sehingga. Sehingga
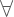
: Untuk Semua.

: Ada. Beberapa. Ada x anggota dari bilangan bulat sehingga x ditambah 1 sama dengan nol.


: Dan. x sama dengan 5 dan x sama dengan 7.
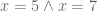

: Atau. n sama dengan 1 atau n sama dengan 4.
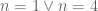
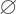
: Himpunan kosong

: Himpunan kosong

: Himpunan bagian
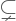
: Bukan himpunan bagian
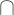
: Irisan

: Gabungan

: Komplemen. Komplemen dari A
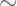
: Sebangun

: Kongruaen. Sama dan sebangun

: Ekuivalen

: Rho
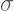
: Sigma
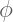
: Phi. Nilai Phi mendekati 1,61803…
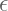
: Epsilon

: Theta
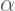
: Alpha
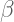
: Beta

: Gamma
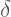
: Delta
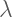
: Lambda

: Perbandingan antara keliling suatu lingkaran dengan diameternya. Nilainya mendekati 3,141592653589…

: Basis logaritma natural. Nilainya mendekati 2,7182818…

: Omega

: Miu

: Tak hingga
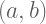
: Suatu selang terbuka. Untuk sebarang x dalam selang, sama dengan

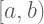
: Suatu selang. Setengah terbuka
![(a,b] (a,b]](http://s0.wp.com/latex.php?latex=%28a%2Cb%5D&bg=ffffff&fg=555555&s=2)
: Suatu selang. Setengah terbuka
![[a,b] [a,b]](http://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=555555&s=2)
: Selang tertutup
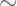
: Negasi. Negasi dari A,

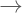
: Jika … maka … . Jika a maka b.


: Jika dan hanya jika … maka … . Jika dan hanya jika m maka n.
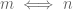
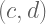
: Faktor persekutuan terbesar dari c dan d. FPB
![[c,d] [c,d]](http://s0.wp.com/latex.php?latex=%5Bc%2Cd%5D&bg=ffffff&fg=555555&s=2)
: Kelipatan persekutuan terkecil dari c dan d. KPK

: Kombinasi
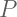
: Permutasi
Tambahan :
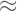
: Mendekati. Suatu nilai, misalnya
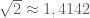
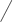
: bukan. Selain. Misalnya,
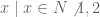
, yaitu semua anggota di himpunan N, kecuali 1 dan 2
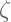
: Zeta
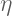
: Eta
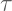
: Tau
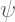
: Psi
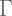
: Gamma. Gamma fungsi.
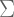
: Sigma

: Omega

: Delta

: Segitiga. Contoh :
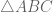
, artinya segitiga ABC

: nabla



















0 komentar:
Posting Komentar